交流阻抗法是电化学测试技术中一类十分重要的方法,是研究电极过程动力学和表面现象的重要手段。特别是近年来,由于频率响应分析仪的快速发展,交流阻抗的测试精度越来越高,超低频信号阻抗谱也具有良好的重现性,再加上计算机技术的进步,对阻抗谱解析的自动化程度越来越高,这就使我们能更好地理解电极表面双电层结构,活化钝化膜转换,孔蚀的诱发、发展、终止以及活性物质的吸脱附过程。
1. 阻抗谱中的基本元件
交流阻抗谱的解析一般通过等效电路来进行,其中基本元件包括:纯电阻R,阻抗值为R;纯电容C,阻抗值为1/jωC;纯电感L,其阻抗值为jωL。实际测量中,将某一频率为ω的微扰正弦波信号施加到电解池,这时可把双电层看成一个电容,把电极本身、溶液及电极反应所引起的阻力均视为电阻,则等效电路如图1所示。
图1.用大面积惰性电极为辅助电极时电解池的等效电路
图中AB分别表示电解池的研究电极和辅助电极两端,Ra, Rb分别表示电极材料本身的电阻,Cab表示研究电极与辅助电极之间的电容,Cd与Cd’表示研究电极和辅助电极的双电层电容,Zf与Zf’表示研究电极与辅助电极的交流阻抗。通常称为电解阻抗或法拉第阻抗,其数值取决于电极动力学参数及测量信号的频率,Rs表示辅助电极与工作电极之间的溶液电阻。一般将双电层电容Cd与法拉第阻抗的并联称为界面阻抗Z。
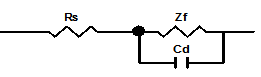
实际测量中,电极本身的内阻很小,且辅助电极与工作电极之间的距离较大,故电容Cab一般远远小于双电层电容Cd。如果辅助电极上不发生电化学反应,即Zf’特别大,又使辅助电极的面积远大于研究电极的面积(例如用大的铂黑电极),则Cd’很大,其容抗Xcd’比串联电路中的其他元件小得多,因此辅助电极的界面阻抗可忽略,于是图1可简化成图2,这也是比较常见的等效电路。
图2.用大面积惰性电极为辅助电极时电解池的简化电路
2. 阻抗谱中的特殊元件
以上所讲的等效电路仅仅为基本电路,实际上,由于电极表面的弥散效应的存在,所测得的双电层电容不是一个常数,而是随交流信号的频率和幅值而发生改变的。一般来讲,弥散效应主要与电极表面电流分布有关。在腐蚀电位附近,电极表面上阴、阳极电流并存,当介质中存在缓蚀剂时,电极表面就会为缓蚀剂层所覆盖,此时,铁离子只能在局部区域穿透缓蚀剂层形成阳极电流,这样就导致电流分布极度不均匀,弥散效应系数较低。表现为容抗弧变“瘪”,如图3所示。另外电极表面的粗糙度也能影响弥散效应系数变化,一般电极表面越粗糙,弥散效应系数越低。
2.1 常相位角元件(Constant Phase Angle Element,CPE)
在表示弥散效应时,近来提出了一种新的电化学元件CPE,CPE的等效电路解析式为:
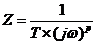 CPE的阻抗由两个参数来定义,即CPE-T,CPE-P,我们知道,
CPE的阻抗由两个参数来定义,即CPE-T,CPE-P,我们知道,
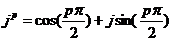 因此CPE元件的阻抗Z可以表示为:
因此CPE元件的阻抗Z可以表示为:
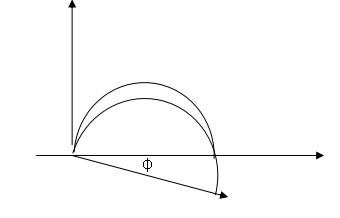
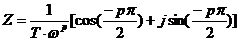 这一等效元件的幅角为φ=-pπ/2,由于它的阻抗的数值是角频率ω的函数,而它的幅角与频率无关,故文献上把这种元件称为常相位角元件。
实际上,当p=1时,如果令T=C,则有Z=1/(jωC),此时CPE相当于一个纯电容,波特图上为一个在第一象限的半圆,相应电流的相位超过电位正好90度,当p=-1时,如果令T=1/L,则有Z=jωL,此时CPE相当于一个纯电感,波特图上为一在第四象限的正半圆,相应电流的相位落后电位正好90度;当p=0时,如果令T=1/R,则Z=R,此时CPE完全是一个电阻。
一般当电极表面存在弥散效应时,CPE-P值总是在1~0.5之间,阻抗波特图表现为向下旋转一定角度的半圆图。
这一等效元件的幅角为φ=-pπ/2,由于它的阻抗的数值是角频率ω的函数,而它的幅角与频率无关,故文献上把这种元件称为常相位角元件。
实际上,当p=1时,如果令T=C,则有Z=1/(jωC),此时CPE相当于一个纯电容,波特图上为一个在第一象限的半圆,相应电流的相位超过电位正好90度,当p=-1时,如果令T=1/L,则有Z=jωL,此时CPE相当于一个纯电感,波特图上为一在第四象限的正半圆,相应电流的相位落后电位正好90度;当p=0时,如果令T=1/R,则Z=R,此时CPE完全是一个电阻。
一般当电极表面存在弥散效应时,CPE-P值总是在1~0.5之间,阻抗波特图表现为向下旋转一定角度的半圆图。
图3. 具有弥散效应的阻抗图
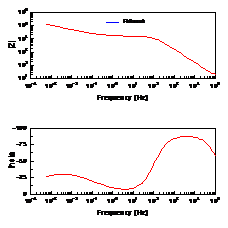
可以证明,弥散角φ=π/2*(1-CPE-P),特别有意义的是,当CPE-P=0.5时,CPE可以用来取代有限扩散层的Warburg元件。 Warburg元件是用来描述电荷通过扩散穿过某一阻挡层时的电极行为。在极低频率下,带电荷的离子可以扩散到很深的位置,甚至穿透扩散层,产生一个有限厚度的Warburg元件。如果扩散层足够厚或者足够致密,将导致即使在极限低的频率下,离子也无法穿透,从而形成无限厚度的Warburg元件,而CPE正好可以模拟无限厚度的Warburg元件的高频部分。当CPE-P=0.5时, 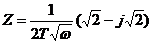 ,其阻抗图为图4所示,一般在pH>13的碱溶液中,由于生成致密的钝化膜,阻碍了离子的扩散通道,因此可以观察到图4所示的波特图。
,其阻抗图为图4所示,一般在pH>13的碱溶液中,由于生成致密的钝化膜,阻碍了离子的扩散通道,因此可以观察到图4所示的波特图。
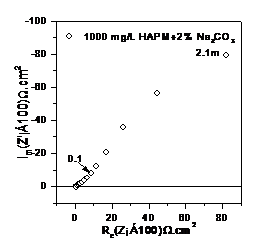
图4 当CPE-P为0.5时(左)及在Na2CO�3溶液中的波特图
2.2 有限扩散层的Warburg元件-闭环模型
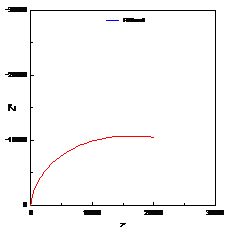
本元件主要用来解析一维扩散控制的电化学体系,其阻抗为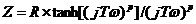 ,一般在解析过程中,设置P=0.5,并且Ws-T=L2/D,(其中L是有效扩散层厚度,D是微粒的一维扩散系数),计算表明,当ω->0时,Z=R,当ω->+∞,在
,一般在解析过程中,设置P=0.5,并且Ws-T=L2/D,(其中L是有效扩散层厚度,D是微粒的一维扩散系数),计算表明,当ω->0时,Z=R,当ω->+∞,在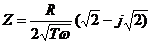 ,与CPE-P=0.5时的阻抗表达式相同,阻抗图如图5。
,与CPE-P=0.5时的阻抗表达式相同,阻抗图如图5。
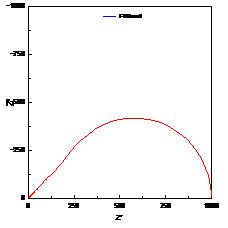
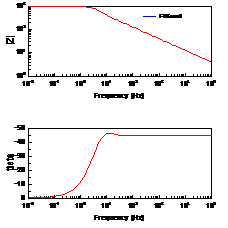
图5. 闭环的半无限的Warburg阻抗图
2.3 有限扩散层的Warburg元件-发散模型
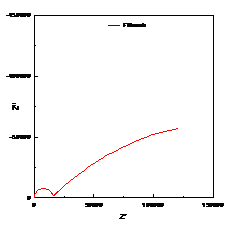
本元件也是用来描述一维扩散控制的电化学体系,其阻抗为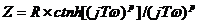 ,其中ctnh为反正切函数,F(x)=Ln[(1+x)/(1-x)]。与闭环模型不同的是,其阻抗图的实部在低频时并不与实轴相交,而是向虚部方向发散。即在低频时,更像一个电容。典型的阻抗图如图6。
,其中ctnh为反正切函数,F(x)=Ln[(1+x)/(1-x)]。与闭环模型不同的是,其阻抗图的实部在低频时并不与实轴相交,而是向虚部方向发散。即在低频时,更像一个电容。典型的阻抗图如图6。
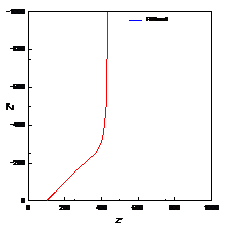
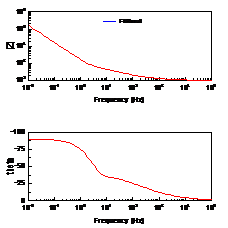
图6. 发散的半无限的Warburg阻抗图
3. 常用的等效电路图及其阻抗图谱
对阻抗的解析是一个十分复杂的过程,这不单是一个曲线拟合的问题。事实上,可以选择多个等效电路来拟合同一个阻抗图,而且曲线吻合得相当好,但这就带来了另外一个问题:哪一个电路符合实际情况呢?这其实也是最关键的问题。实验者需要有相当丰富的电化学知识,并且对所研究体系有比较深刻的认识,而且在复杂的情况下,单纯依赖交流阻抗是难以解决问题的,需要辅助以极化曲线以及其他暂态实验方法。
由于阻抗测量基本是一个暂态测量,所以对工作电极、辅助电极以及参比电极的鲁金毛细管位置极有要求。例如鲁金毛细管距离工作电极的位置不同,在阻抗图的高频部分就会表现出很大的差异,距离远时,高频部分仅出现半个容抗弧,距离近时,高频弧变成一个封闭的弧;当毛细管紧挨着工作电极表面时,可能会出现感抗弧,这其中原因还不清楚。
为了有利于大家在今后的实验中对阻抗图有一个粗略的认识,下面简单将几种常见阻抗图谱介绍一下。
3.1 吸附型缓蚀剂体系
如果缓蚀剂不参与电极反应,不产生吸附络合物等中间产物,则它的阻抗图仅有一个时间常数,表现为变形的单容抗弧。这是由于缓蚀剂在表面的吸附会使弥散效应增大,同时也使双电层电容值下降,其阻抗图及其等效电路如图7。
图7. 具有一个时间常数的单容抗弧阻抗图
3.2 涂层下的金属电极阻抗图
涂装金属电极存在两个容性时间常数,一个是涂层本身的电容,另外一个是金属表面的双电层电容,阻抗图上具有双容抗弧,如图8所示:
等效电路中的Ccoat为涂层本身的电容,Rcoat为涂层电阻,Cdl为涂层下的双电层电容。当溶液通过涂层渗透到金属表面时,还会有电化学反应发生,Rcorr为电极反应的阻抗。
3.3 局部腐蚀的电极阻抗图
当金属表面存在局部腐蚀(点腐蚀),点蚀可描述为电阻与电容的串联电路,其中电阻Rpit为蚀点内溶液电阻,一般Rpit=1~100Ω之间。实际体系测得的阻抗应为电极表面钝化面积与活化面积(即点蚀坑)的界面阻抗的并联耦合。但因钝化面积的阻抗远远高于活化面的阻抗,因而实际上阻抗频谱图反映了电极表面活化面积上的阻抗,即两个时间常数叠合在一起,表现为一个加宽的容抗弧。其阻抗图谱与等效电路如图9所示。
3.4 半无限扩散层厚度的电极阻抗图
所谓半无限扩散过程,是指溶液中的扩散区域,即在定态下扩散粒子的浓度梯度为一定数值的区域,扩散层厚度为无穷大。不过一般如果扩散层厚度大于数厘米后,即可认为满足这一条件。此时法拉第阻抗就等于半无限扩散控制的浓差极化阻抗Zw与电极反应阻抗Zf的串联,其阻抗
电极反应完全受扩散步骤控制,外加的交流信号只会引起表面反应粒子浓度的波动,且电极表面反应粒子的浓度波动相位角正好比交流电流落后45度,阻抗图为45度角的倾斜直线,如图10所示。如果法拉第阻抗中有Warburg阻抗,则Rp→无穷大,但在腐蚀电位下,由于总的法拉第阻抗是阳极反应阻抗与阴极反应阻抗的并联,一般仅有阴极反应有Zw,故此时总的Rp应为阳极反应的Rp1值,Zf仍为有限值。
当电极表面存在较厚且致密的钝化膜时,由于膜电阻很大,离子的迁移过程受到极大的抑制,所以在低频部分其阻抗谱也表现为一45度倾角的斜线。
3.5 有限扩散层厚度的电极阻抗图
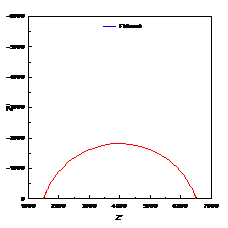
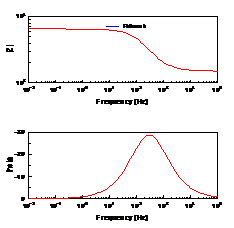
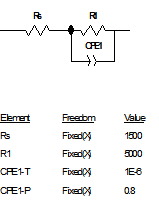
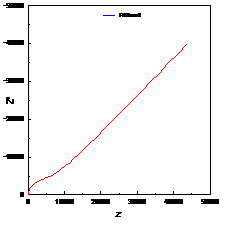
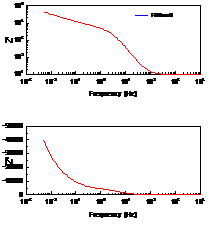
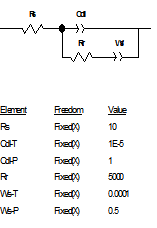
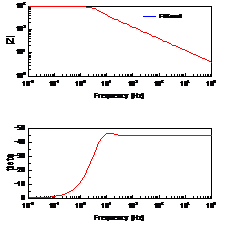
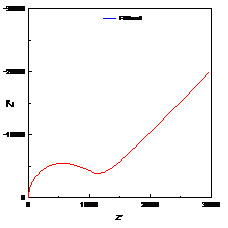
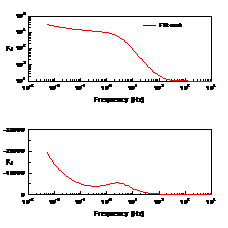
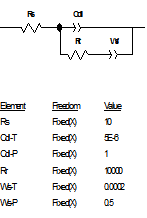
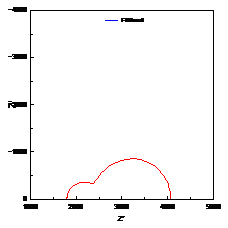
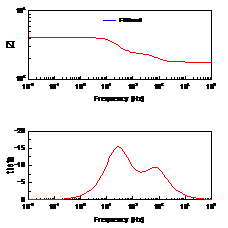
当扩散层厚度有限时,即在距离电极表面x=l处,扩散粒子的浓度为一个不随时间变化的定值,则有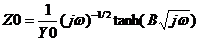 ,在低频是完全由浓差扩散控制,但在高频时它相当于一个RC串联电路,见2.2节。实际测量中,当电极表面存在扩散层控制时,在较低频率下,离子的迁移过程可以通过延长时间来扩散到金属表面,发生电化学反应,因此波特图表现为一闭合的圆弧,可以用有限扩散层厚度的Warburg阻抗来模拟,如图11所示。
,在低频是完全由浓差扩散控制,但在高频时它相当于一个RC串联电路,见2.2节。实际测量中,当电极表面存在扩散层控制时,在较低频率下,离子的迁移过程可以通过延长时间来扩散到金属表面,发生电化学反应,因此波特图表现为一闭合的圆弧,可以用有限扩散层厚度的Warburg阻抗来模拟,如图11所示。
3.6 同时受电化学和浓差极化控制
在混合控制下,交流信号通过电极时,除了浓差极化外还将出现电化学极化,这时电极的法拉第阻抗比较复杂;在高频部分为双电层的容抗弧,而在低频部分,扩散控制将超过电化学控制,出现Warburg阻抗,其等效电路及阻抗图如图12所示。
3.7 具有双容抗弧的电化学阻抗
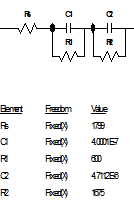
另外如果法拉第电流If不仅与极化电位DE有关,而且与某一表面状态变量X相关,则由于X对电位的响应会引起弛豫现象,从而出现除双电层电容以外的第二个时间常数。不过,该常数既可能是容性的也可能是感性的,这取决于B值。当B>0时,低频出现感抗弧,当B<0时,则在低频出现第二个容抗弧。某些吸附型物质在电极表面成膜后,这层吸附层覆盖于紧密双电层之上,且其本身就具有一定的容性阻抗Cf,它与电极表面的双电层串联在一起组成具有两个时间常数的阻抗谱,其阻抗图如图13所示。
3.8 低频出现感抗弧的电化学体系
前面说过,如果法拉第电流不仅与电极电位有关,而且受电极表面状态变量X影响,而这个状态变量本身又是电极电位E的函数,则会有
式中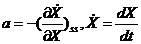 当B>0时,
当B>0时, 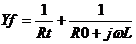 ,低频部分出现感抗弧。
当电极反应出现中间产物时,这种中间产物吸附于金属电极表面,产生表面吸附络合物。该表面络合物产生于电极反应的第一步,而消耗于第二步反应。而一般情况下,吸附过程的弛豫时间常数要比电双层电容Cdl与Rt组成的充放电过程的弛豫时间常数大得多,因此在阻抗图的低频部分会出现感抗弧。如图14所示。
当B<0时,上式可改写为
进一步可以得到法拉第阻抗
,低频部分出现感抗弧。
当电极反应出现中间产物时,这种中间产物吸附于金属电极表面,产生表面吸附络合物。该表面络合物产生于电极反应的第一步,而消耗于第二步反应。而一般情况下,吸附过程的弛豫时间常数要比电双层电容Cdl与Rt组成的充放电过程的弛豫时间常数大得多,因此在阻抗图的低频部分会出现感抗弧。如图14所示。
当B<0时,上式可改写为
进一步可以得到法拉第阻抗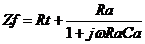 ,这相当于RC并联电路,即法拉第阻抗本身具有一个时间常数,加上双电层电容,整个EIS出现两个容抗弧,如图13所示。
4. 混合电位下的阻抗谱特征
上面所述的阻抗谱均是在自然电位下测量的,而电极反应在自然电位下同时具有阴、阳极两个反应,所以阻抗谱所反映的是两个电极反应的频谱特征,即文献所述的混合电位下的阻抗谱。当没有状态变量时,EIS仍只有一个时间常数,当有一个状态变量影响电极反应速度时,阻抗谱会出现两个时间常数。不过在某些情况下,需要研究单一阳极反应特征,就必须将研究电极的电位极化(弱极化区)到不同的阳极电位下进行阻抗测量,以抑制阴极反应,这就是所谓的直流偏压下的阻抗测试。这一点对于研究钝化膜的临界破裂电位下的阻抗特征尤为重要,它能提供点蚀诱发期的重要特征,另外在研究缓蚀剂的阳极脱附行为时也十分重要。
5. 交流阻抗的不足之处
前面指出,对于同一阻抗谱,可以找到不止一个等效电路满足它的解析,而对于同一个电路,当电路中的元件参数不同时,可以得到完全不同类型的阻抗谱,因此依靠等效电路来推测电极过程的动力学机构是不可靠的。
附录: ZView电化学阻抗分析软件使用说明
1. Zview拟合快速指南
,这相当于RC并联电路,即法拉第阻抗本身具有一个时间常数,加上双电层电容,整个EIS出现两个容抗弧,如图13所示。
4. 混合电位下的阻抗谱特征
上面所述的阻抗谱均是在自然电位下测量的,而电极反应在自然电位下同时具有阴、阳极两个反应,所以阻抗谱所反映的是两个电极反应的频谱特征,即文献所述的混合电位下的阻抗谱。当没有状态变量时,EIS仍只有一个时间常数,当有一个状态变量影响电极反应速度时,阻抗谱会出现两个时间常数。不过在某些情况下,需要研究单一阳极反应特征,就必须将研究电极的电位极化(弱极化区)到不同的阳极电位下进行阻抗测量,以抑制阴极反应,这就是所谓的直流偏压下的阻抗测试。这一点对于研究钝化膜的临界破裂电位下的阻抗特征尤为重要,它能提供点蚀诱发期的重要特征,另外在研究缓蚀剂的阳极脱附行为时也十分重要。
5. 交流阻抗的不足之处
前面指出,对于同一阻抗谱,可以找到不止一个等效电路满足它的解析,而对于同一个电路,当电路中的元件参数不同时,可以得到完全不同类型的阻抗谱,因此依靠等效电路来推测电极过程的动力学机构是不可靠的。
附录: ZView电化学阻抗分析软件使用说明
1. Zview拟合快速指南
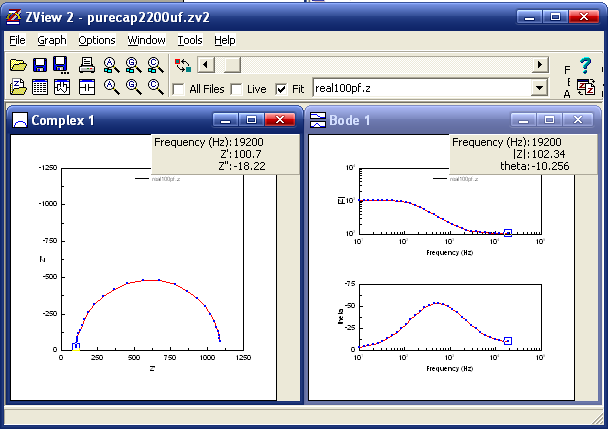
ZView是一款功能较强的电化学阻抗分析与绘图软件,能对EIS数据进行各种电化学参数计算,还能对电位、电流原始数据进行平滑和数字滤波处理,同时还可以通过软件方式补偿溶液电阻。ZView操作界面简单明了,数据、图形可以方便地打印和存储,并可以矢量方式输出到Word文档中,其良好的帮助系统能回答用户在使用过程中的大部分问题。
图1-1. Zview阻抗分析界面
工具条按钮实际上是菜单的快捷键,如果鼠标停留在工具条图标上,则会出现相关文字说明,所有图标的功能均可通过菜单实现。工具条也包括了几种不同的功能,下面将按其功能分类详细说明。
图1-2.工具条详细说明
打开+保存图形文档:用于加载ZView文档,一个文档包括了重绘图形的相关信息。
打印图形:打印当前选定的图形;
重画坐标:提供了几种用于重画图形坐标的方法;
数据显示:决定调入的数据如何显示,以及数据光标的控制;
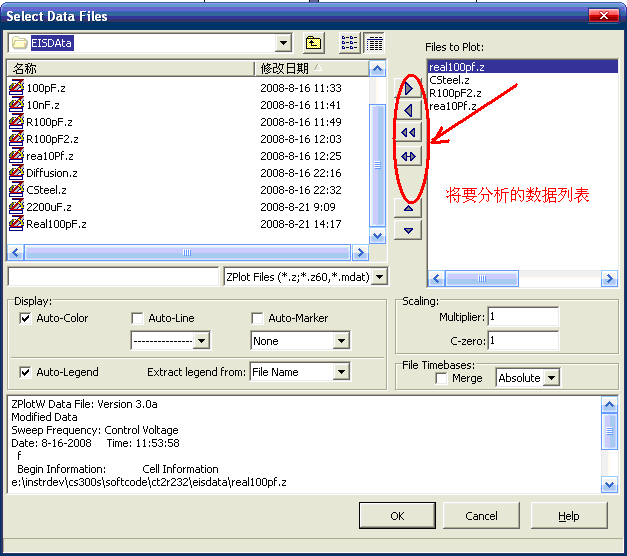
1.1 打开数据文件,从菜单“File”-“Data File”将阻抗数据文件通过箭头导入到右边列表中,如下图3。
图1-3. Zview导入数据文件窗口
1.2 激活数据,从图4中的“1”位置的下拉框中选择将要分析的数据。
图1-4. Zview中选择活动的数据
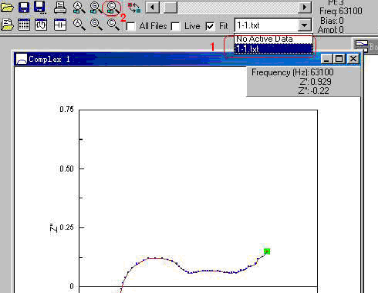
1.3 删除不需要的数据,通过光标选择不需要的数据段,也就是Zview不能拟合的部分,然后用菜单Tools��→“Delete Data Range”删除之。
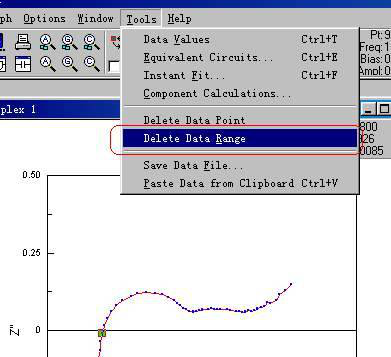
图1-5. 从Zview中选择要删除的数据段演示图
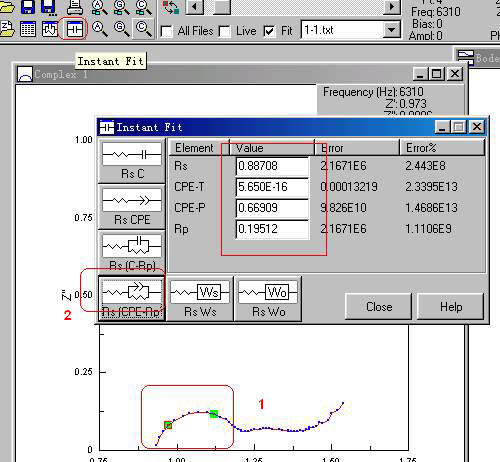
1.4 快速拟合,也就是为后面正式拟合获取初值:
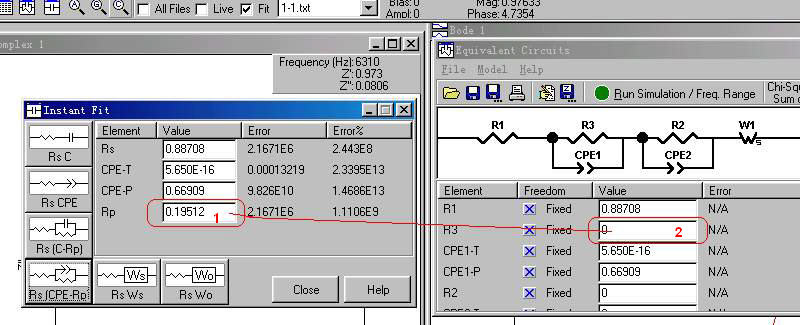
1)这个需要一个一个元件单独进行,如图1-6中“2”处所标,选中部分准备进行即时拟合;
2)在左上角打框的地方(Instant Fit),点击它就是快速拟合。
3)选择适宜的等效元件,如“2”处所标识,获得等效电路的初值。
图1-6. 从Zview中选择即时拟合等效电路来确定拟合初值演示图
1.5 建立适宜的等效电路,如图1-7,这个取决于用户的测试体系,详情参见Zview在线帮助。
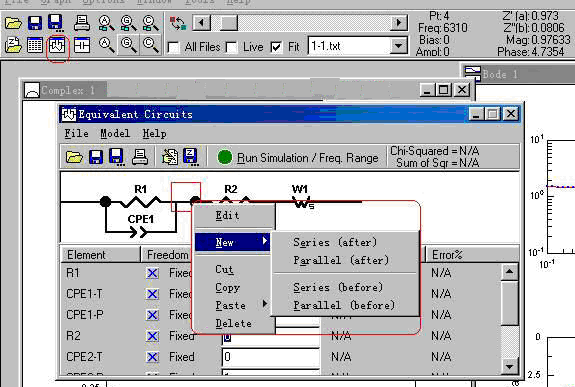
图1-7. 从Zview中选择合适的等效电路来进行正式拟合演示图
1.6 把图1-8中“1”处的数据用鼠标拖到到“2”处位置。
图1-8. 从快速拟合窗口中将数据传送到等效电路拟合的初值输入框演示图
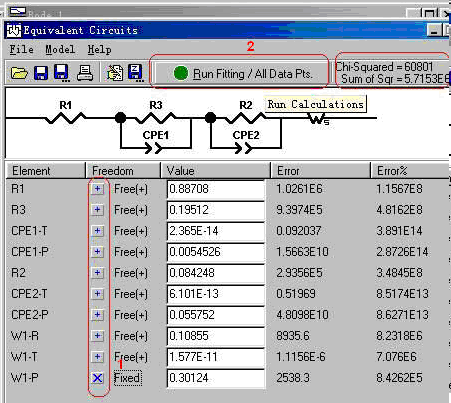
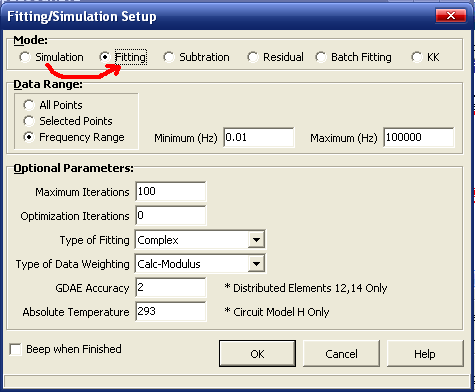
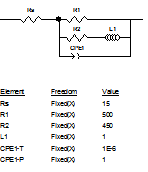
1.7把图1-9中的“1”处的Fixed改成Free,为拟合作准备,同时需要将等效电路拟合窗口(如图1-10)中的mode由“Simulation 改选为“Fitting”才能拟合。
图1-9. 根据建立的等效电路进行数据拟合演示图
图1-10. 拟合窗口参数设置
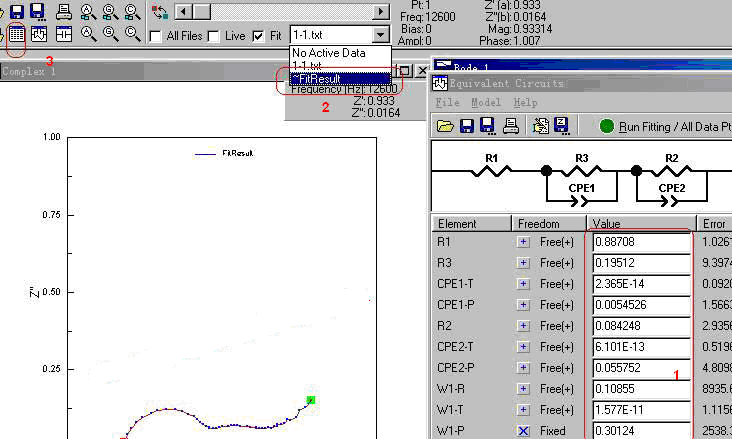
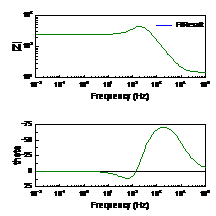
1.8如图1-11的“1”处是拟合的结果,如果要用拟合得到数据绘图,则在“2”处选拟合结果,再点击“3”处。
图1-11. 拟合数据结果以及拟合曲线



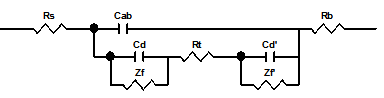
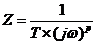
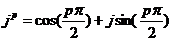
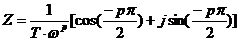
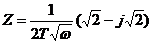 ,其阻抗图为图4所示,一般在pH>13的碱溶液中,由于生成致密的钝化膜,阻碍了离子的扩散通道,因此可以观察到图4所示的波特图。
,其阻抗图为图4所示,一般在pH>13的碱溶液中,由于生成致密的钝化膜,阻碍了离子的扩散通道,因此可以观察到图4所示的波特图。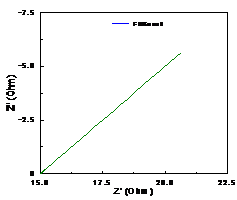
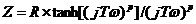 ,一般在解析过程中,设置P=0.5,并且Ws-T=L2/D,(其中L是有效扩散层厚度,D是微粒的一维扩散系数),计算表明,当ω->0时,Z=R,当ω->+∞,在
,一般在解析过程中,设置P=0.5,并且Ws-T=L2/D,(其中L是有效扩散层厚度,D是微粒的一维扩散系数),计算表明,当ω->0时,Z=R,当ω->+∞,在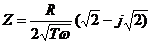 ,与CPE-P=0.5时的阻抗表达式相同,阻抗图如图5。
,与CPE-P=0.5时的阻抗表达式相同,阻抗图如图5。

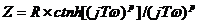 ,其中ctnh为反正切函数,F(x)=Ln[(1+x)/(1-x)]。与闭环模型不同的是,其阻抗图的实部在低频时并不与实轴相交,而是向虚部方向发散。即在低频时,更像一个电容。典型的阻抗图如图6。
,其中ctnh为反正切函数,F(x)=Ln[(1+x)/(1-x)]。与闭环模型不同的是,其阻抗图的实部在低频时并不与实轴相交,而是向虚部方向发散。即在低频时,更像一个电容。典型的阻抗图如图6。


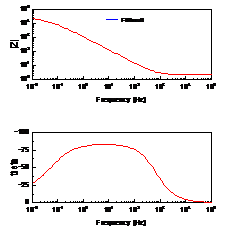

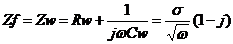
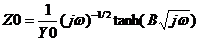 ,在低频是完全由浓差扩散控制,但在高频时它相当于一个RC串联电路,见2.2节。实际测量中,当电极表面存在扩散层控制时,在较低频率下,离子的迁移过程可以通过延长时间来扩散到金属表面,发生电化学反应,因此波特图表现为一闭合的圆弧,可以用有限扩散层厚度的Warburg阻抗来模拟,如图11所示。
,在低频是完全由浓差扩散控制,但在高频时它相当于一个RC串联电路,见2.2节。实际测量中,当电极表面存在扩散层控制时,在较低频率下,离子的迁移过程可以通过延长时间来扩散到金属表面,发生电化学反应,因此波特图表现为一闭合的圆弧,可以用有限扩散层厚度的Warburg阻抗来模拟,如图11所示。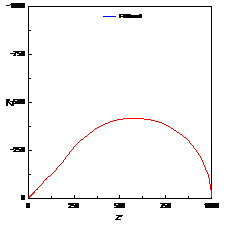

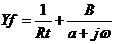
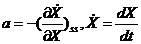
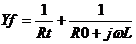 ,低频部分出现感抗弧。
,低频部分出现感抗弧。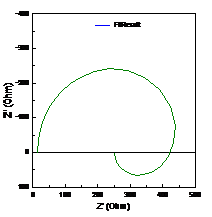
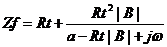
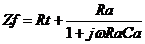 ,这相当于RC并联电路,即法拉第阻抗本身具有一个时间常数,加上双电层电容,整个EIS出现两个容抗弧,如图13所示。
,这相当于RC并联电路,即法拉第阻抗本身具有一个时间常数,加上双电层电容,整个EIS出现两个容抗弧,如图13所示。